A álgebra nas profissões

3º DIA

A álgebra na carpintaria

Será que a álgebra tem vez em uma simples carpintaria?
Tem sim. Existem problemas que o marceneiro pode resolver de forma muito eficiente com auxílio da álgebra. Vamos ver um deles.

EXEMPLO 3

O corte está no lugar certo?
Certo dia, um marceneiro recebeu a seguinte tarefa: cortar os cantos de uma mesa quadrada, que tinha 120 cm de lado, para transformÆ-la em uma outra com 8 lados iguais.
Observe, nas figuras abaixo, o problema do marceneiro.

Repare que o problema de transformar a mesa quadrada em outra, com 8 lados iguais, não é um problema fácil.  Os cortes precisam ser feitos em lugares certos.  Se não, o marceneiro corre o risco de estragar a mesa. Como fazer, então,os cortes perfeitos?

Acompanhe o raciocínio do marceneiro e, mais uma vez, a utilidade da álgebra.

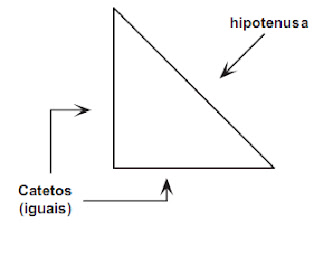
As partes que serão eliminadas da mesa quadrada são triângulos retângulos com dois lados iguais. Eles se chamam catetos. O lado maior, onde será feito o corte, chama-se hipotenusa

Para observar direito esse triângulo, ele fez um desenho grande de um triângulo desse tipo, com catetos de 1 m de comprimento, e mediu a hipotenusa.

O valor que ele encontrou para a hipotenusa foi 1 metro e 41 centímetros (este valor não é exato, porém é bem aproximado).
O marceneiro sabia que, para aumentar ou diminuir o tamanho de uma figura, mantendo sua forma, basta multiplicar  todos os comprimentos dessa figura por um mesmo número. Por exemplo, um triângulo 10 vezes maior que o da figura que o marceneiro fez terá lados de 10 m, 10 m e 14,1 m.
Ele, então, raciocinou corretamente colocando a letra x como a medida dos catetos dos triângulos que serão retirados. Assim, a medida da hipotenusa desses triângulos será 1,41x.
Veja como ficou o projeto da nova mesa.

Na mesa de 8 lados, todos eles devem ser iguais. Portanto, a medida de cada um deles será 1,41x.
Agora, basta somar os comprimentos sobre um lado do quadrado antigo.

x  +  1,41x  +  x   =   120 

Agora, vamos envolver essa equação.

2x   +  1,41x  = 120

           3,41x  = 120

           3,41x = 120
              3,41      3,41   

                    x = 35,19

Concluímos, então, que cada cateto dos triângulos que serão retirados mede, aproximadamente, 35,2 cm. O problema está resolvido. A partir de cada canto da mesa, o marceneiro vai medir comprimentos de 35,2 cm, e passar a serra nas hipotenusas dos triângulos formados.
A mesa ficará com 8 lados iguais. E qual será a medida de cada lado da nova mesa?

Cada lado da nova mesa mede 1,41x, ou seja, 1,41 · 35,2, o que dá 49,6 cm.
Quase 50 cm de lado.

Como você percebeu, a álgebra foi utilizada para resolver problemas muito diferentes. Mas não se esqueça: ela é apenas uma ferramenta. O mais importante é sempre o raciocínio. 

A habilidade de resolver problemas se desenvolve aos poucos. Com a prática. Com persistência.